1789. Степень перестановки
Найдите степень заданной
перестановки p.
Перестановкой из n элементов
называется упорядоченный набор из n различных чисел от 1 до n.
Степенью перестановки p называется
такое минимальное натуральное число k, что pk = ε,
где ε – тождественная перестановка (1, 2, ..., n).
Вход. Первая строка содержит натуральное
число n (0 < n ≤ 100) – размер перестановки p. Вторая
строка содержит саму перестановку p, представленную в виде
последовательности из n чисел.
Выход. Выведите степень заданной
перестановки.
|
Пример
входа 1 |
Пример
выхода 1 |
64 3 2 5 1 6 |
6 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
94 3 6 8 9 7 2 1 5 |
12 |
РЕШЕНИЕ
комбинаторика
- перестановки
Анализ алгоритма
Пусть p –
заданная перестановка, а p[i]
– элемент перестановки, находящийся в позиции i. Рассмотрим последовательность элементов: i, p[i], p[p[i]], … . Поскольку количество элементов
в перестановке конечно, существует такое минимальное k, что p[i]k = i.
Последовательность элементов i, p[i], p[p[i]], …, p[i]k-1, для которой p[i]k = i, будем называть циклом. Длина
цикла равна k.
Любую
перестановку можно представить в виде списка циклов. Например, перестановка [4, 3, 2, 5, 1, 6] представляется
как (1, 4, 5)(2, 3)(6).
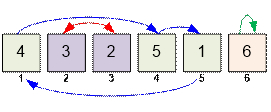
Например, последовательность
(1, p[1], p[p[1]]) = (1, 4, 5) образует цикл, так как p[p[p[1]]]
= p[1]3 = 1. Длина этого цикла равна 3.
Степень перестановки равна НОК
длин ее циклов.
Пример
В первом примере
перестановка [4, 3, 2, 5, 1, 6] представляется в виде (1, 4, 5)(2,
3)(6). Длины
циклов равны 3, 2 и 1. Степень перестановки равна НОК(3, 2, 1) = 6.
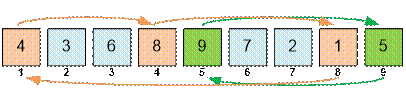
Во втором
примере перестановка [4, 3, 6, 8, 9, 7, 2, 1, 5] представляется в виде (1, 4, 8)(2, 3,
6, 7)(5, 9). Длины
циклов равны 3, 4 и 2. Степень перестановки равна НОК(3, 4, 2) = 12.
Реализация алгоритма
Массив p хранит входную перестановку. Массив used
используется для
пометки обработанных элементов.
#define MAX 101
int p[MAX], used[MAX];
Читаем входную перестановку.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&p[i]);
В
переменной res подсчитываем степень перестановки p.
res = 1;
memset(used, 0, sizeof(used));
Перебираем
индексы перестановки. Для каждого обработанного индекса i устанавливаем used[i] = 1.
for (i = 1; i <= n; i++)
if (!used[i])
{
Цикл
с элементом p[i] еще не обнаружен. Ищем длину цикла len в
перестановке, начиная с индекса j = i. Для этого последовательно
переходим по индексам j, p[j], p[p[j]], …, пока не встретится уже
пройденный элемент. Все пройденные индексы j
отмечаем как посещённые, устанавливая used[j] = 1.
len = 0;
j = i;
while (!used[j])
{
used[j] = 1;
j = p[j];
len++;
}
Переменная
len содержит длину текущего найденного цикла. Вычисляем НОК
длин всех циклов.
res = lcm(res, len);
}
Выводим ответ.
printf("%d\n", res);